1、曲率(外文名:curvature)是描述几何体弯曲程度的量,例如曲面偏离平面的程度,或者曲线偏离直线的程度。在不同的几何学领域中,曲率的具体定义不完全相同。曲率可分为外在曲率和内蕴曲率,二者有重要的区别。前者的定义需要把几何体嵌入到欧氏空间中,后者则是直接定义在黎曼流形上。
2、正曲率:负曲率曲面上的三角形三角之和大于平面三角形的三角之和。负曲率:负曲率曲面上的三角形三角之和小于平面三角形的三角之和。参考资料来源:百度百科-高斯曲率 参考资料来源:百度百科-曲率 正曲率和负曲率是描述曲线或曲面形状的术语,它们区别如下: 正曲率:正曲率表示曲线或曲面在某一点处向外凸出,呈现出向外的弯曲形状。
3、在微分几何中,曲率是描述曲线或曲面在某一点处的弯曲程度的量。对于曲线,我们通常使用一阶导数来计算曲率;而对于曲面,我们则使用二阶导数来计算曲率。
4、曲率是描述曲线弯曲程度的一个物理量,是在某一点上曲线的弯曲程度的倒数,也可以理解为曲线在该点上的圆弧半径。在平面直角坐标系中,曲线上一点的曲率圆方程为:(x - a)^2 + (y - b)^2 = 1 / |k| 其中,(a, b)是曲线上该点的坐标,|k|是曲线在该点处的曲率的绝对值。
5、曲率的定义:曲线的曲率定义为曲线上某点切线方向角对弧长的转动率,它通过微分来量化曲线偏离直线的程度。数学上,曲率是曲线在某一点弯曲程度的数值表示。曲率越大,表示曲线的弯曲程度也越大。曲率的倒数称为曲率半径,它谈明曲线变得多么“平缓”。
6、曲率是针对曲线上某个点的切线方向角对弧长的转动率,通过微分来定义,表明曲线偏离直线的程度。数学上表明曲线在某一点的弯曲程度的数值。曲率越大,表示唤穗曲线的弯曲程度越大。曲率的倒数就是曲率半径。
1、曲线的曲率(curvature):就是针对曲线上某个点的切线方向角对弧长的转动率。通过微分来定义就是:K=lim|Δα/Δs|,Δs趋向于0的时候,k值就是曲率。曲率表明曲线偏离直线的程度,或曲线在某一点的弯曲程度的数值。曲率越大,表示曲线的弯曲程度越大。曲率半径:曲率的倒数就是曲率半径。曲率半径求法:ρ=|[(1+y';^2)^(3/2)/y';';]|,K=1/ρ。
2、曲线的曲率就是针对曲线上某个点的切线方向角对弧长的转动率,通过微分来定义,表明曲线偏离直线的程度。数学上表明曲线在某一点的弯曲程度的数值。曲率越大,表示曲线的弯曲程度越大.无限曲率就是指一个物体在做无止境的不规则的曲线动动。
3、曲率是针对曲线上某个点的切线方向角对弧长的转动率,通过微分来定义,表明曲线偏离直线的程度。数学上表明曲线在某一点的弯曲程度的数值。曲率越大,表示唤穗曲线的弯曲程度越大。曲率的倒数就是曲率半径。
1、在二维平面上,曲线的曲率被定义为曲线在该点的斜率的倒数。而在三维空间中,曲率则描述了空间曲线在该点的空间弯曲程度。首先,我们从二维平面的情况开始。曲率公式是描述曲线在某一点的弯曲程度的数学工具。
2、= (1 + y';^2)^(3/2)/ y';';曲率就是1/r;有了半径r、法线斜率(-1/y';),就很容易的求出曲率圆的圆心了,继而求出曲率圆的方程。不知道对你有帮助没有。
3、性质曲率越大:表示曲线的弯曲程度越大。曲率半径:曲率的倒数即为曲率半径。曲率半径越小,表示曲线在该点附近弯曲得越厉害。计算公式设曲线的直接坐标方程为 $y = f(x)$,且 $f(x)$ 具有二阶导数 $f';';(x)$。曲线在点 $M(x, y)$ 处的切线的斜率为 $k = f';(x)$。
4、由于f(x)在曲线上,可以将f(x)视为曲线的纵坐标y,于是f';(x)就是曲线在该点处的斜率,f';';(x)就是曲线在该点处的曲率的导数。
5、曲率(外文名:curvature)是描述几何体弯曲程度的量,例如曲面偏离平面的程度,或者曲线偏离直线的程度。在不同的几何学领域中,曲率的具体定义不完全相同。曲率可分为外在曲率和内蕴曲率,二者有重要的区别。前者的定义需要把几何体嵌入到欧氏空间中,后者则是直接定义在黎曼流形上。
6、斜率相当于坐标轴,曲率相当于切线。根据查询作业帮显示:斜率相当于坐标轴,曲率相当于切线。斜率由速度变化问题和曲线的切线问题而抽象出来的数学概念。又称变化率。曲率是针对曲线上某个点的切线方向角对弧长的转动率,通过微分来定义,表明曲线偏离直线的程度。
1、在微分几何学中,曲率是衡量曲线或曲面在某一点弯曲程度的一个重要指标。对于平面曲线,曲率定义为针对曲线上某个点的切线方向角对弧长的转动率。这意味着,曲率可以直观理解为曲线偏离直线的程度。具体地,曲率的倒数即为曲率半径,用公式表示为R=1/K。
2、曲率半径为曲率的倒数。在微分几何中,曲率的倒数就是曲率半径,即R=1/K。平面曲线的曲率定义为曲线上一点的切向角对弧长的微分旋转率,表示曲线偏离直线的程度。对于曲线,它等于靠近该点曲线的圆弧半径。曲率半径求法:ρ=||,K=1/ρ。
3、曲率的计算公式是κ=y';';/(1+(y';)²)^(3/2),其中,κ为曲率,y';为函数y的导数,y';';为函数y的二阶导数。这个公式描述了曲线上某一点处的曲率,即曲线在该点处的弯曲程度。曲率是微分几何中的一个基本概念,它描述了曲线或曲面在某一点处的弯曲程度。
4、 曲率的定义 在微分几何中,曲率用于描述曲线或曲面在特定点的弯曲程度。 曲率越大,表示曲线在该点的弯曲程度越高。 曲率的计算 对于平面曲线,曲率的计算涉及曲线的切线方向的变化率,具体可通过计算曲线的导数变化率来得到。 在三维空间中,曲面的曲率计算更为复杂,包括主曲率、平均曲率等概念。
5、在微分几何中,曲率的倒数就是曲率半径,即R=1/K。平面曲线的曲率就是针对曲线上某个点的切线方向角对弧长的转动率,通过微分来定义,表明曲线偏离直线的程度。对于曲线,它等于最接近该点处曲线的圆弧的半径。 对于表面,曲率半径是最适合正常截面或其组合的圆的半径。
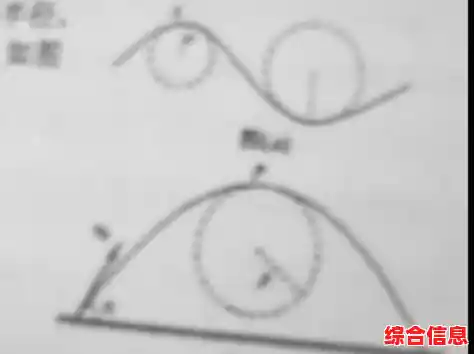
6、本文主要讨论的内容是:可微参数曲线的定义、曲线的曲率、曲线的扰率、正则曲面的定义、第一基本形式、第二基本形式。 在实践过程中,我们要处理的大多数曲线都是参数曲线,而且都是可微的,所以,给一个参数曲线的定义不如给一个可微参数曲线的定义。
1、曲率是针对曲线上某个点的切线方向角对弧长的转动率,通过微分来定义,表明曲线偏离直线的程度。数学上表明曲线在某一点的弯曲程度的数值。曲率越大,表示唤穗曲线的弯曲程度越大。曲率的倒数就是曲率半径。
2、曲线的曲率就是针对曲线上某个点的切线方向角对弧长的转动率,通过微分来定义,表明曲线偏离直线的程度。数学上表明曲线在某一点的弯曲程度的数值。曲率越大,表示曲线的弯曲程度越大.无限曲率就是指一个物体在做无止境的不规则的曲线动动。
3、曲线的曲率就是针对曲线上某个点的切线方向角对弧长的转动率,通过微分来定义,表明曲线偏离直线的程度。数学上表明曲线在某一点的弯曲程度的数值。曲率越大,表示曲线的弯曲程度越大。曲率的倒数就是曲率半径,即R=1/K。
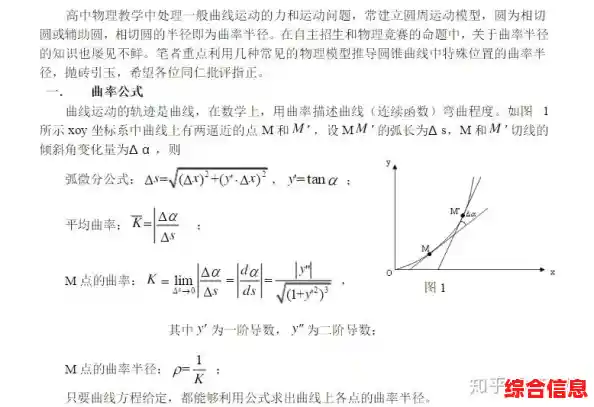
4、曲线的曲率(curvature):就是针对曲线上某个点的切线方向角对弧长的转动率。通过微分来定义就是:K=lim|Δα/Δs|,Δs趋向于0的时候,k值就是曲率。曲率表明曲线偏离直线的程度,或曲线在某一点的弯曲程度的数值。曲率越大,表示曲线的弯曲程度越大。曲率半径:曲率的倒数就是曲率半径。曲率半径求法:ρ=|[(1+y';^2)^(3/2)/y';';]|,K=1/ρ。
5、曲率是用来表示曲线弯曲程度的量。平面曲线的曲率定义为曲线上某个点的切线方向角对弧长的转动率,通过微分来定义,用来衡量曲线偏离直线的程度。曲率越大,表明曲线的弯曲程度越高。曲率的计算公式为K=lim|Δα/Δs|,当Δs趋向于0时,定义K就是曲率。
1、定义:曲线的曲率是针对曲线上某个点的切线方向角对弧长的转动率。这个公式通过微分来定义,表明了曲线偏离直线的程度。物理意义:曲率是几何体不平坦程度的一种衡量。在动力学中,一个物体相对于另一个物体做变速运动时,由于时空扭曲,也会产生曲率。
2、在微分几何中,曲率的倒数就是曲率半径,即R=1/K。平面曲线的曲率就是针对曲线上某个点的切线方向角对弧长的转动率,通过微分来定义,表明曲线偏离直线的程度。对于曲线,它等于最接近该点处曲线的圆弧的半径。 对于表面,曲率半径是最适合正常截面或其组合的圆的半径。
3、曲线的曲率就是针对曲线上某个点的切线方向角对弧长的转动率,通过微分来定义,表明曲线偏离直线的程度。数学上表明曲线在某一点的弯曲程度的数值。曲率越大,表示曲线的弯曲程度越大 曲率的求法如下:曲率半径求法:ρ=|[(1+y';^2)^(3/2)/y';';]|,K=1/ρ。
4、曲率的一种直观解读方式是密切圆的半径的倒数,即:kappa = frac{1}{R} 这里,$R$是密切圆的半径。直线的曲率为$1/infty = 0$,表示直线不弯曲;而圆的曲率则是其半径的倒数,半径越大,曲线看起来越不弯曲。
1、曲线向下凸起,曲率半径为负。同样地,在三维空间中,曲线的凹凸性与曲率的正负也有关系。当曲线在某一点处向上凸起时,该点处的曲率为正;当曲线在某一点处向下凸起时,该点处的曲率为负。总而言之,曲率的正负与曲线的凹凸性有关,曲线凹向上方时曲率为正,曲线凸向上方时曲率为负。
2、正曲率和负曲率是描述曲线或曲面的特征,它们之间的区别在于曲线或曲面的弯曲方向。正曲率表示曲线或曲面向外弯曲,类似于一个凸出的形状。在正曲率的情况下,曲线或曲面上的切线向外弯曲,曲率半径为正值。例如,球体表面就具有正曲率,因为它在每个点上都向外凸出。
3、正曲率:意味着宇宙空间呈球状。在这种情况下,空间弯曲会导致光线沿着曲线行进,形成“引力弯曲”。光线在宇宙中回转,最终可能返回初始位置,形成“宇宙循环”。正曲率的宇宙结构是封闭的,物质也会沿着这样的曲线在宇宙中移动,形成闭合宇宙。负曲率:表示空间呈现马鞍状。
4、指代不同 正曲率:对曲线上某个点的切线方向角对弧长的转动率为正值。负曲率:对曲线上某个点的切线方向角对弧长的转动率为负值。几何体描述不同 正曲率:曲面上的三角形的内角和大于π。负曲率:负曲率曲面上的三角形的内角和小π。